NAVEGAÇÃO LOXODRÔMICA

 

O autor desta página com a colaboração
de Wikiwand e Wikipédia

Navegação loxodromica e ortodromica

PRELIMINARES

Em matemática, a trigonometria esférica estuda as propriedades geométricas dos triângulos esféricos, em especial as relações que envolvem ângulos esféricos e arcos esféricos. É a área da geometria esférica que estuda os polígonos que se formam sobre a superfície das esferas, em especial, os triângulos. O estudo de trigonometria esférica tem especial relevância em náutica e navegação para determinar a posição de uma embarcação em alto-mar mediante a observação dos corpos celestes.

A ESFERA

Uma esfera E, de centro no ponto (a,b,c) e raio k, é domínio de R³ definido por todos pontos no espaço tridimensional que cumprem com a seguinte definição:

$${\displaystyle E=\{\ (x,y,z)\in \mathbb {R} ^{3}\ |\ (x-a)^{2}+(y-b)^{2}+(z-c)^{2}=k^{2}\}.}$$

CÍRCULO MÁXIMO

A intersecção de uma esfera com um plano que contenha seu centro gera um círculo máximo e uma circunferência máxima sobre a superfície da esfera. Um círculo máximo divide a esfera em dois hemisférios iguais. A distância entre dois pontos da superfície da esfera, unidos por um arco de círculo máximo, é a menor entre eles, e denomina-se distancia ortodrômica. Como exemplos de círculos máximos, temos na superfície terrestre os meridianos e a linha do equador.

TRIÂNGULO ESFÉRICO

Triângulo esférico.

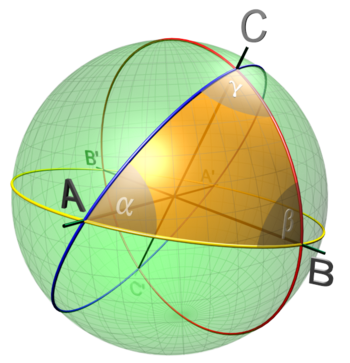
Se três pontos da superfície esférica são unidos por arcos de círculo máximo, menores que 180º, a figura obtida denomina-se triângulo esférico. Os lados do polígono assim formado se expressam por conveniência como ângulos cujos vértices são o centro da esfera e não por sua longitude. Este arco medido em radianos e multiplicado pelo raio da esfera é a longitude do arco. Em um triângulo esférico os ângulos cumprem que: 180° < ${\displaystyle \alpha }$ + ${\displaystyle \beta }$ + ${\displaystyle \gamma }$ < 540°.

FÓRMULAS FUNDAMENTAIS

•  ângulo formado entre os arcos AC e AB
• ${\displaystyle \beta$ :} ângulo formado entre os arcos AB e BC
• ${\displaystyle \gamma$ :} ângulo formado entre os arcos AC e BC

Wikiwand, informa

Observe-se que, nos cálculos a seguir, supõe-se que a distância D seja expressa em graus. O fator de transformação entre milhas náuticas e graus é:

1 milha náutica = 1/60 graus

Além disso, assume-se que os ângulos, bem como os argumentos das funções trigonométricas, são expressos em graus. Consequentemente, os resultados das funções trigonométricas inversas serão graus.

CLASSES DE DERROTAS

A derrota a ser seguida pelo naviopode ser loxodrômica ou ortodrômica (circulo máximo). A derrota loxodrômica corta todos os meridianos terrestres sob um mesmo ângulo , chamado ângulo de rumo verdadeiro ou rumo verdadeiro. mas, não representa a distância mais curta entre dois pontos. Para obter a distância mais curta entre dois pontos devemos nos valer da derrota ortodrômica. Ao se percorrer um meridiano ou o equador ambas derrotas se complementam; em todos os demais casos, navegação ortodrômica sempre se desvia no sentido do polo mais elevado, desvio este maior que o estimado por loxodromia.

ESTIMANDO O RUMO POR NAVEGAÇÃO LOXODRÔMICA:

Fig. 1

Ponto de saída (φs e λs), rumo do navio α e distância a ser percorrida. Estimar (φe e λe).

O método comunmente usado é da latitud média onde se determinará o valor do apartamento, cateto oposto (Δl da Fig.1), por meio da expressão: D x sen.rumo.

então, 

Δl =  D x sen.α [1]

Δφ = D x cos.α [2]

sempre lembrando que α é o rumo atual do navio 

A latitude média se obterá somando a latitude se saída com a metade da diferença em latitude (metade de Δl da Fig.1). O valor da latitude média obtido é indispensável para determinação da diferença de longitude, que será obtida por: apartamento x sec.latitude média.

então, fica assim:

φm = φs + Δφ/2 [3]

Δλ =  Δl x sec.φm [4]

Finalmente somando as diferenças em latitude e em longitude  aos valores de latitude e longitude de saída se obteram a latitude e longitude estimados: 

φe = φs +  Δφ [5]

λe = λs + Δλ    [6]

As expressoes [1] e [4] a miude são reunidas em uma única expressão para cálculos logarítmicos e então fica assim:

Δλ = D x sen.rumo x sec.latitude média

Em todas estas expressões o sinal mais indica que estes valores devem somar-se algebricamente, isto é levando em conta seu próprio sinal.

Saindo do porto de Helgoland (54º 11' N e 7º 53' E) navegou-se no rumo verdadeiro de 316º (N 44º W) uma distância de 447 milhas, estimou-se a a posição do navio.

Helgoland  é um pequeno arquipélago no Mar do Norte

assim:

φs = 54º 11' N                    λs = 7º 53' E

Δφ = 5º 22' N                     Δλ = 9º 28' W

φe = 59º 33' N                    λe = 1º 35' W

Δφ/2 = 2º 41'

φm = 56º 52'

A = 310,5

Δλ = 568,1

log sec = 0,26234

log = 2,49206

log = 2,75410

Das tabelas de estima extraímos:

α = 316º

d = 447 milhas

Δφ = 321,6'

A = 310,5

Concluindo:

316º d = 200 milhas                    Δφ = 143,9                    A = 138,9

316º d = 247 milhas                    Δφ = 177,7                    A = 171,6

316º d = 447 milhas                    Δφ = 321,6                    A = 310,5

O cálculo da diferença em longitude, a partir do apartamento, se calculará logaritmicamente somente nas grandes distâncias; para pequenas distâncias se resolverá mediante as tabelas de estima como a seguir:

Ainda, saindo de Helgoland (54º 11' N e 7º 53' E) navegou-se no rumo verdadero de 316º (N 44º W) uma distância de 36 milhas. A posição achada foi:

α = 316º

d = 36 milhas

Δφ = 25,9'

A = 25,0'

 φs = 54º 11' N                    λs = 7º 53' E

 Δφ = 26 N                          Δλ =     43 W

φe = 54º 37' N                    λe = 7º 10' E

A Equação Loxodrome na Projeção de Mercator

Para encontrar a equação de um loxodromo conectando dois pontos arbitrários na superfície da Terra, a localização dos dois pontos pode ser transferida para uma grade de Mercator. Uma linha reta conectando os dois pontos na grade de Mercator representa o loxodromo e o ângulo sob o qual esta linha reta se cruza com uma linha vertical (Meridiano) é o verdadeiro curso para esta linha de rumo.

A transformação de Mercator pode ser descrita da seguinte forma: duas localizações arbitrárias L0 e L1 são especificadas por suas coordenadas de Latitude e Longitude na superfície da Terra:

  Localização L0: ( Lat0 , Lon0 )
  Local L1: ( Lat1 , Lon1 )
ver Fig.2 

A transformação de Mercator mapeia esses pontos em uma carta náutica de Mercator plana (X,Y):

  Localização L0: X0 = Lon0 ; Y0 = ln(tan( Lat0 /2+45°)) * 57,2958
  Localização L1: X1 = Lon1 ; Y1 = ln(tan( Lat1 /2+45°) ) * 57,2958
Fig.2
O fator "57,2958" é um fator de escala para garantir a conformidade. 
É determinado por 180°/PI = 57,2958°/rad. 
Esta escala do eixo Latitude assegura que - no Equador - a distância de um grau de Latitude 
é igual à distância de um grau de Longitude.