ESTABILIDADE DO NAVIO: CURVA GZ
Curva GZ é uma curva que indica a distância transversal entre o centro de gravidade (G) e o centro de flutuabilidade (B) em uma condição em que a embarcação está inclinada em um determinado ângulo.
O estaleiro fornece as informações para calcular GZ para vários ângulos de adernamento e para vários deslocamentos.
O trim do navio geralmente é zero para a confecção das tabelas hidrostáticas.
Todas as indicações são para condições estáticas do mar. Esta é a razão pela qual a curva também é chamada de curva de estabilidade estática.
Qual é o propósito de fornecer informações da curva GZ em um navio?
O objetivo das informações da curva GZ é:
Demonstrar o cumprimento dos critérios de estabilidade intacta em qualquer condição de serviço.
Demonstrar o cumprimento dos critérios de estabilidade em avaria em situação de rompimento do casco.
Para encontrar o efeito de; deslocamento transversal e vertical de um peso; efeito de superfície livre; efeito do aterramento na curva GZ.
Qual é o significado da área sob a curva GZ?
A área sob a curva GZ é uma medida da estabilidade dinâmica de um navio.
A estabilidade dinâmica em um ângulo pode ser entendida como a energia necessária ou o trabalho realizado por uma agência externa para inclinar o navio até aquele ângulo.
Matematicamente, isso é igual ao produto do deslocamento da embarcação pela área sob a curva em metros – radianos.
A área sob a curva é normalmente encontrada pelas regras de Simpson. A curva GZ indica o potencial de estabilidade e, portanto, a capacidade do navio de resistir ao adernamento em condições de mar agitado.
Que informações estão disponíveis em uma curva GZ?
As seguintes informações estão disponíveis em uma curva GZ:
O GM inicial: A inclinação da curva GZ na origem é indicativa de ‘Estabilidade inicial’ (GM0).
Braço de endireitamento máximo: É a distância vertical máxima ou separação da curva GZ da linha de base.
O momento máximo de endireitamento: Pode ser encontrado multiplicando o GZ máximo pelo deslocamento.
Os ângulos de equilíbrio: Os ângulos de inclinação nos quais a curva GZ toca o eixo x ou a linha de base são os ângulos nos quais o navio pode estar em equilíbrio.
A faixa de estabilidade positiva: é a faixa em graus entre o ângulo de equilíbrio vertical e o ângulo de estabilidade nula.
Ângulo de imersão da borda do tabuleiro: O ponto em que a concavidade muda para convexidade é denominado ponto de contraflexão. Isso ocorre aprox. na imersão da borda do convés.
Ângulo de adernamento máximo que a embarcação pode sustentar: Baseia-se no princípio de que se o momento de inclinação causado for maior que o momento máximo de endireitamento o navio virará.
Ângulo de adernamento perigoso: Alguns dizem que o ângulo metade do ângulo de adernamento máximo permitido é o ângulo de perigo limite da lista.
Ângulo de inclinação para a condição de vertical negativo GM0: A curva GZ faz um loop na direção negativa e então sobe novamente para cima, cruzando o eixo x no ângulo de inclinação.
O ângulo de inclinação devido ao fato de G estar fora do centro: É encontrado pela interseção da curva cosseno (GG1 cos θ) com a curva GZ original.
Estabilidade dinâmica: A estabilidade dinâmica em qualquer ângulo de adornamento é encontrada multiplicando a área sob a curva até esse ângulo pelo deslocamento da embarcação.
A estabilidade estática transversal é a capacidade da embarcação de permanecer em pé sob a influência de vários fatores externos e internos. A estabilidade transversal, como sabemos, considera apenas os aspectos de estabilidade no sentido transversal ou no sentido longitudinal.
Voltando ao básico, quando uma embarcação sofre uma perturbação interna ou externa de direção lateral, ela tende a adernar ou tombar para um determinado lado. Mais uma vez, o calcanhar é a inclinação causada por forças externas, e o tombamento se deve à transferência de pesos internos.
A inclinação é medida em termos do ângulo do calcanhar. Os pontos mais importantes a considerar ao analisar a estabilidade inicial intacta são o centro de gravidade, G, o centro de flutuabilidade, B, e o metacentro, M. Ao compreender o metacentro. É importante voltar às condições iniciais de estabilidade.
Assim, o metacentro é o ponto de intersecção da linha central do navio, com a linha passando pelo centro de flutuabilidade quando o navio está inclinado. Aludindo e reiterando às condições iniciais de estabilidade, se o metacentro transversal estiver verticalmente acima do centro de gravidade, diz-se que o navio está num estado estável ou de equilíbrio se o metacentro transversal estiver verticalmente acima do centro de gravidade.
Se o metacentro coincidir com o CG, diz-se que a embarcação está em estado neutro. E se o metacentro estiver abaixo do CG, diz-se que a embarcação está num estado instável. Quando a embarcação está inclinada, uma alavanca ou braço de endireitamento tende a trazer a embarcação de volta à sua posição vertical através do seu momento de endireitamento. O comprimento deste braço é um determinante direto do momento de endireitamento.
Agora, a estabilidade inicial pode estar sob dois tipos de estudo: 1) estabilidade em grandes ângulos de inclinação e 2) estabilidade em pequenos ângulos de inclinação. Embora considere pequenos ângulos de inclinação, geralmente é considerado entre 4 ou 5 graus. Porém, quando o ângulo de inclinação ou lista é maior que 4 ou 5 graus de raio, ele é considerado sob a alçada de ângulos grandes.
Isto porque, tecnicamente, quando os ângulos de inclinação são maiores que este, o metacentro M não permanece um ponto fixo, mas dinâmico. Além disso, já não pode ser considerada uma medida de estabilidade e entram em jogo formulações e cálculos de estabilidade um tanto alterados e mais complicados.
Assim, a determinação da alavanca de endireitamento para estas instâncias requer consideração especial e pode ser estimada usando relações como a fórmula de Atwood ou a fórmula Wall-sided, que é um caso especial de Atwood. Não entramos nas formulações e outros aspectos, pois fogem ao escopo deste artigo.
Agora, para estabilidade em grandes ângulos, surge um caso muito interessante. Como já sabemos pelos primeiros princípios de estabilidade, o braço ou alavanca endireitadora pode ser positivo, negativo ou zero. Um braço de endireitamento positivo cria um momento de endireitamento positivo que tende a levar a embarcação a uma posição vertical a partir de uma posição instável. Em contraste, um momento de endireitamento negativo empurra ainda mais a embarcação para adernar ou tombar para o seu lado.
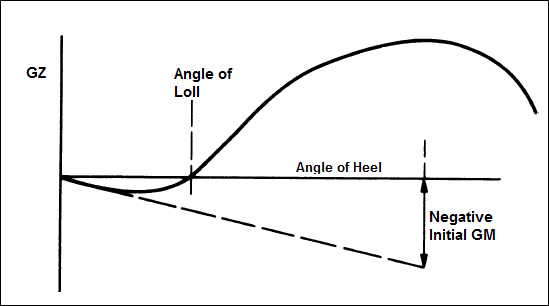
Para a alavanca de endireitamento zero, o caso é bastante complicado. Quando a altura metacêntrica ou GM é positiva ou zero, o braço de alavanca ainda pode ser zero e diz-se que a embarcação está em equilíbrio. Aqui, o navio permanecerá essencialmente na sua posição sem inclinar mais, mas, ao mesmo tempo, sem tendência a voltar a ficar em pé, uma vez que não existe braço de momento para dar origem ao momento crucial necessário.
Ainda assim, a embarcação pode ser considerada mais ou menos 'estável', graças ao GM positivo ou, por outras palavras, à localização do metacentro acima do centro de gravidade, como sabemos. Porém, quando a embarcação tem braço de endireitamento zero e GM negativo, pode haver um caso muito especial que não pode ser considerado um estado instável. Aqui, a embarcação atingirá um estado em que estará em equilíbrio, mas nunca o atingirá! Parece estranho, certo? Mas isso acontece neste caso.
Como o GM é negativo e o BM é positivo, o navio nunca virará, mas tenderá a permanecer num estado de oscilação, ou seja, para frente e para trás. Não haverá preferência pela embarcação em relação a nenhum lado específico. O ângulo de inclinação da embarcação sob determinadas condições em que isso ocorre é conhecido como ângulo de inclinação, e diz-se que a embarcação está em um estado de movimento contínuo de rolamento.
Devido à ausência de uma alavanca estabilizadora de endireitamento acoplada a um GM negativo, a embarcação nunca atingirá a estabilidade ou verticalidade desejada. Isto também é conhecido como estado de equilíbrio instável .
Instável no sentido de que nunca atinge a posição desejada, e equilíbrio no sentido de que mesmo que não o faça, permanece num estado que não se inclina parcialmente para um lado continuamente e vira. Porém, durante esse estado incessante de oscilação, se houver entrada de água no convés por algum motivo, a embarcação poderá virar devido ao acréscimo de cargas e forças.
O ângulo de inclinação para um determinado navio sob determinadas condições pode ser determinado matematicamente pelos valores de GM, da altura metacêntrica e BM, e do raio metacêntrico.
De acordo com a curva GZ, o ângulo de loll ocorre no ponto de inflexão quando o GZ ou a alavanca endireitadora torna-se zero durante a transformação de um valor negativo para um valor positivo. Os outros pontos da curva onde o GZ é zero são quando o navio está em um estado vertical natural que não é perturbado por nenhuma força e tem ângulo de adornamento zero, e o final da curva de estabilidade que também é conhecida como ângulo de estabilidade desaparecendo .
A altura metacêntrica ou GM tem duas vezes em magnitude e é oposta em sinal ou direção sob uma condição suspensa. Não entramos nos cálculos detalhados aqui neste post.
Este estado de oscilação ou rolamento contínuo é bastante precário para passageiros e tripulantes. Pode induzir problemas graves como enjôo, danos a equipamentos/sistemas ou perda de carga e outros itens.
A condição piora ainda mais durante condições climáticas adversas, quando o estado do mar já está perturbado e a embarcação já está sujeita a muitas perturbações. Nessas condições, há chances reais de o navio virar. O ângulo de inclinação é uma consideração muito importante para um designer desde o início.
Vários sistemas, como tanques anti-roll ou outros dispositivos e mecanismos anti-roll, são comuns na maioria dos navios modernos para combater os movimentos de rolamento. No entanto, os navios sempre tomam cuidado para evitar esse ângulo de inclinação para todos os efeitos práticos.




